【図解】円筒の回転体を図示してみよう【東北大2007,名古屋大2011】
SUMMARY
- 立体の回転体を考えるときには、軌跡の重複を意識した空間把握が必要です。
- 今回は東北大と名古屋大の過去問を例に、「円筒の回転体」と「ちくわ型の回転体」を図示していきます。
問題
東北大2007[5]
$A$を$x$軸のまわりに一回転してできる立体の体積を求めよ。
名古屋大2011[1]
$-\dfrac{1}{4} \lt s \lt \dfrac{1}{3}$とする。$xyz$空間内の平面$z=0$の上に長方形
$$R_s = \left\{ ( x , y , 0 ) | 1 \leq x \leq 2+4s , 1 \leq y \leq 2-3s \right\}$$
がある。長方形$R_s$を$x$軸のまわりに1回転してできる立体を$K_s$とする。
(1)
立体$K_s$の体積$V(s)$が最大となるときの$s$の値、およびそのときの$V(s)$の値を求めよ。
(2)
$s$を(1)で求めた値とする。 このときの立体$K_s$を$y$軸のまわりに1回転してできる立体$L$の体積を求めよ。
これらは似ていますが少し異なっていて、東北大は円筒の回転、名古屋大はちくわ形の回転を考えます。
詳しい解説はこちらから(外部リンク)。
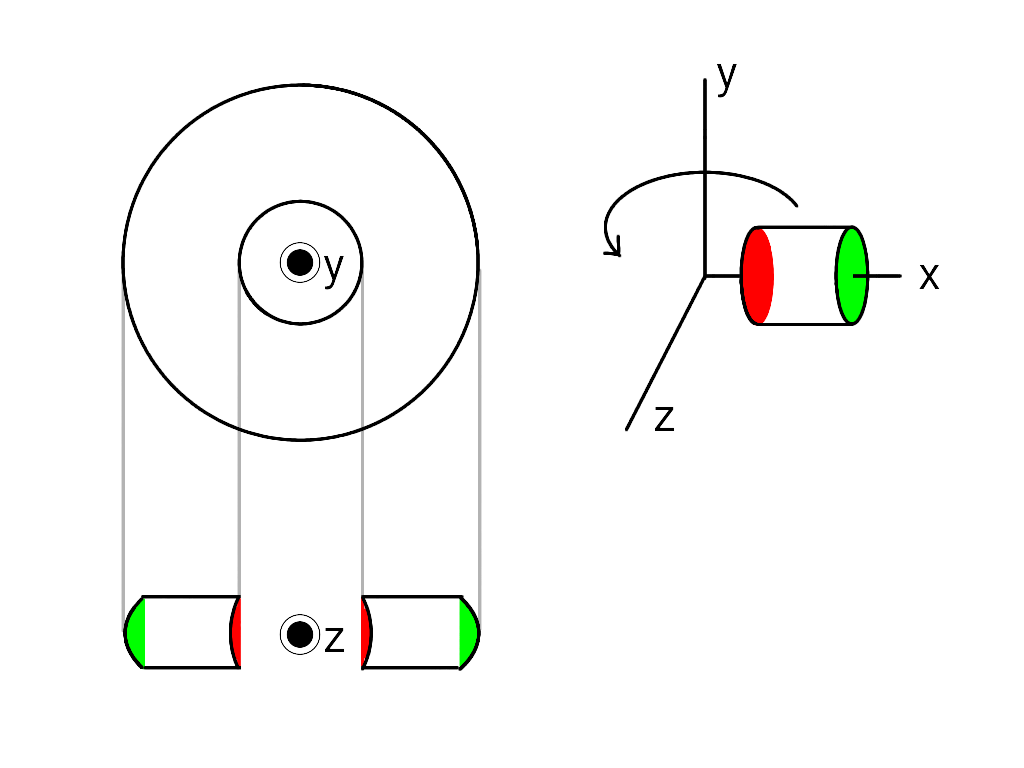
円柱回転体と円筒回転体の体積は違う!!
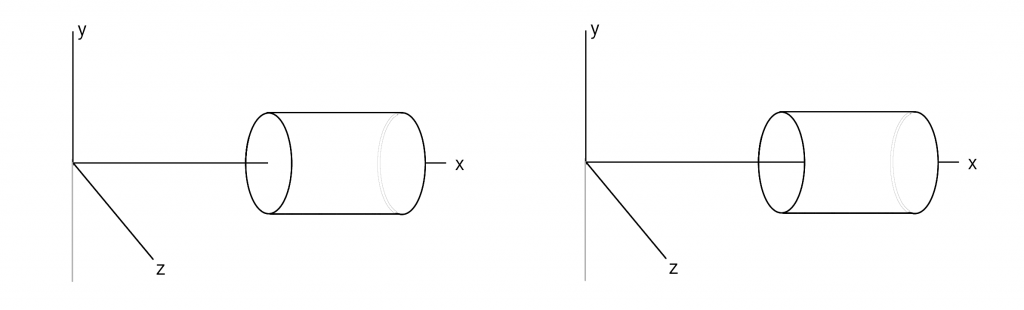
円柱または円筒を、各底面に平行な軸まわりで回転させることを考えます(上の図を例にとると、立体をy軸まわりに回転させます)。
このとき、できあがる立体の体積は「円柱回転体>円筒回転体」となります。
なぜだか分かりますか?
ここが理解できると、上記のような入試問題にも取りかかりやすくなります。
ビジュアル化してみる
こちらの記事にも同様のことを書いていますが、やはり言えることは立体を回転させて立体を作るのはかなり想像しにくいということです。
いわゆる平面図や立面図でイメージがつけばいいのですが、その境地に達するには何かしらの訓練が要ると思います。
円柱を回転させる場合
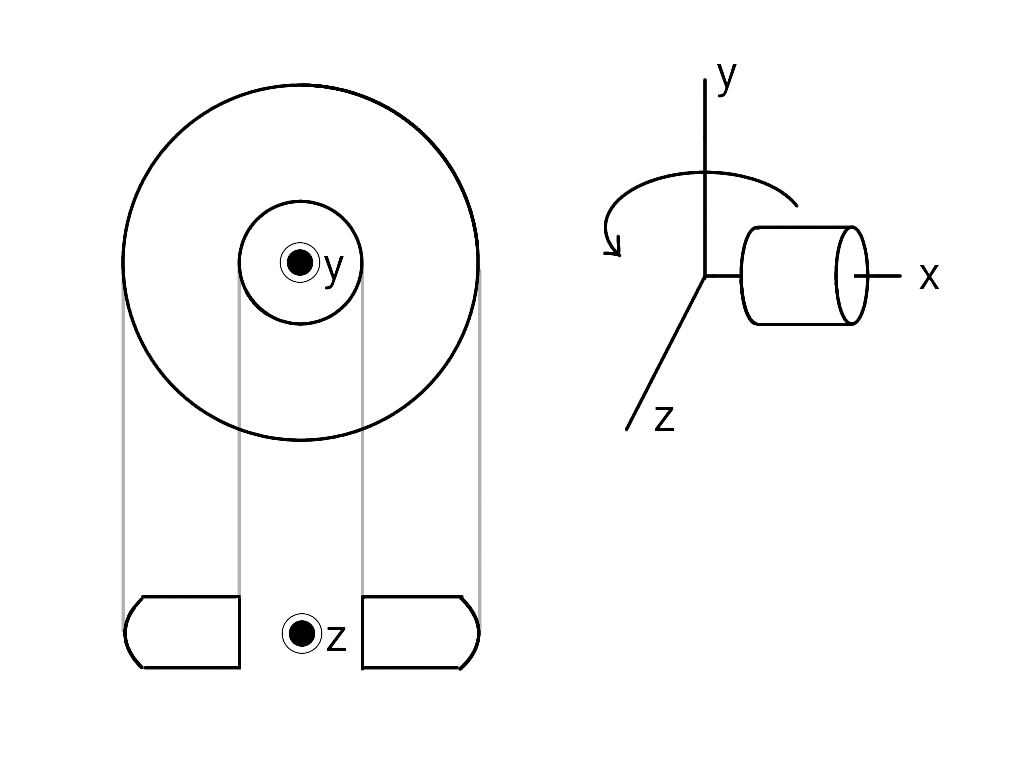
出来上がる立体は、内側は平らで外側は曲がった曲面を描くようなバームクーヘン形です。
円筒を回転させる場合
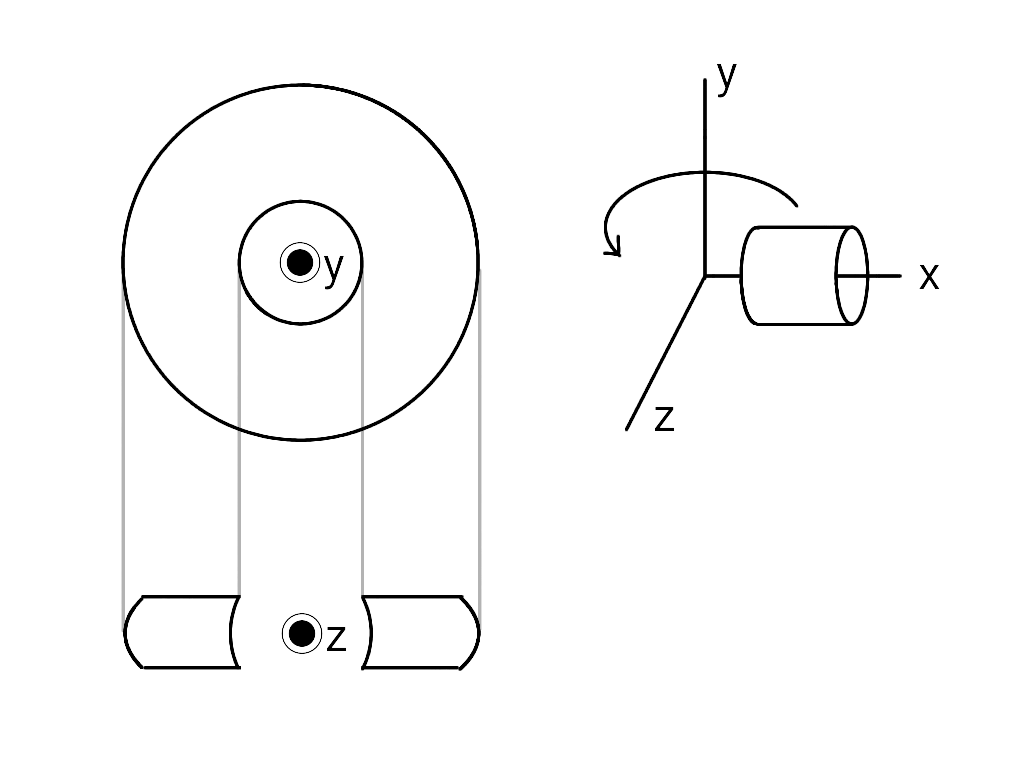
出来上がる立体は、内側も外側も曲がった曲面を描くようなバームクーヘン形です。
内側がえぐれている分、こちらの方が体積が小さくなります。
平面の回転体との関連付け
円筒の回転体を、平面の作る回転体から解釈してみます。
円筒を$xy$面に射影した図形(長方形)の回転体は、立体のうち以下の部分を占めます。
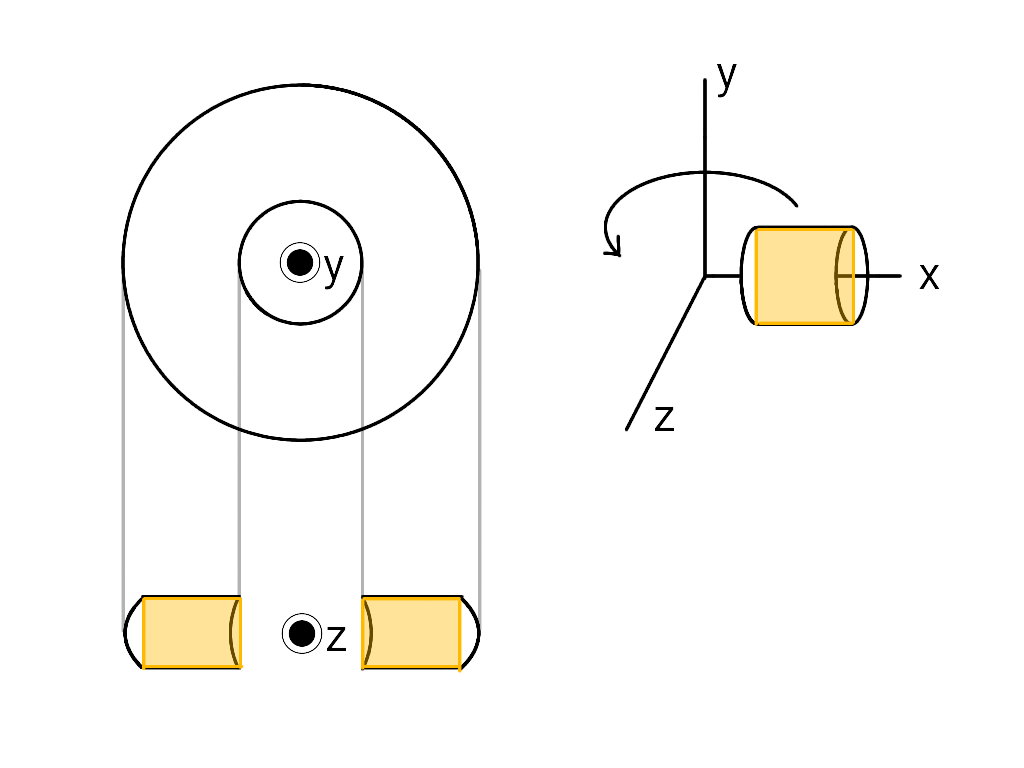
一方、円筒の両端である円の回転体は、立体のうち以下の部分を占めます。
つまり、円筒回転体の体積を求めるには、黄色い長方形の回転体+緑の円の回転体-赤の円の回転体という計算をすればOKです。
なお、カヴァリエリの原理を用いると、緑の円の回転体=赤の円の回転体という結果が得られるので、結局円筒回転体の体積=黄色い長方形の回転体になります。
円筒側面の軌跡
そもそも円筒回転体について「内側が凹むこと」がピンと来ない方もいるかもしれません。
注目する高さ$y$によって、回転半径が変わる様子を見てみましょう。
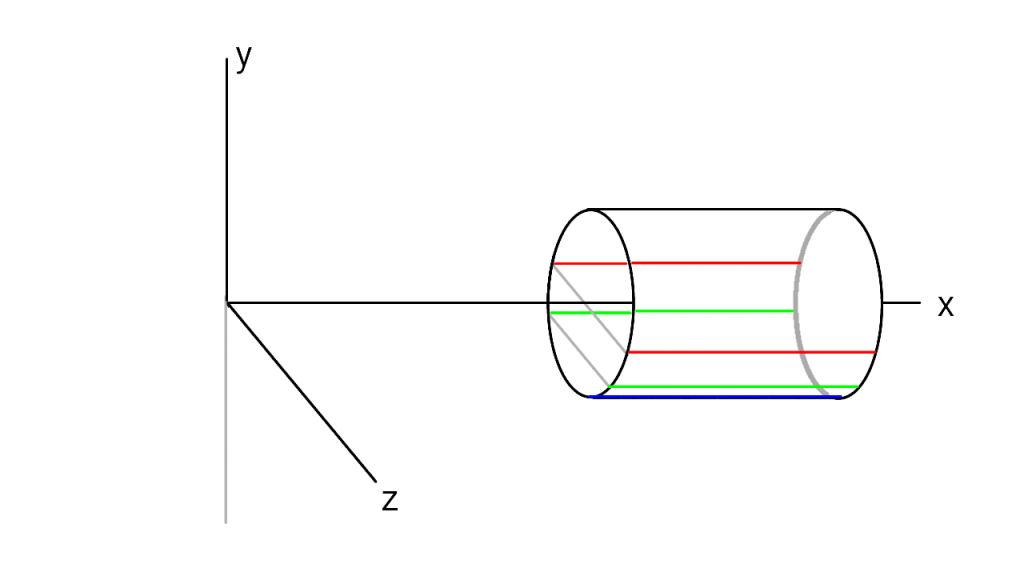
側面上に直線状のマーカーを引きます。
円筒の一番太い部分($y=0$)を赤、下端($y=-r$)を青、その中間($-r<y<0$)を緑としました。
これらの軌跡を見てみます。
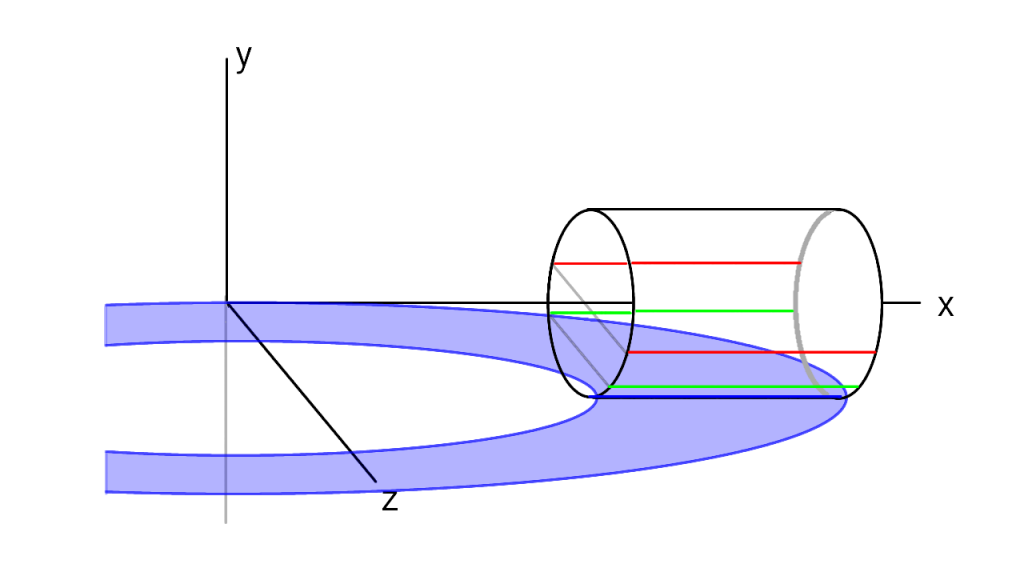
青線の軌跡は単純で、円筒内へのえぐり込みはありません。
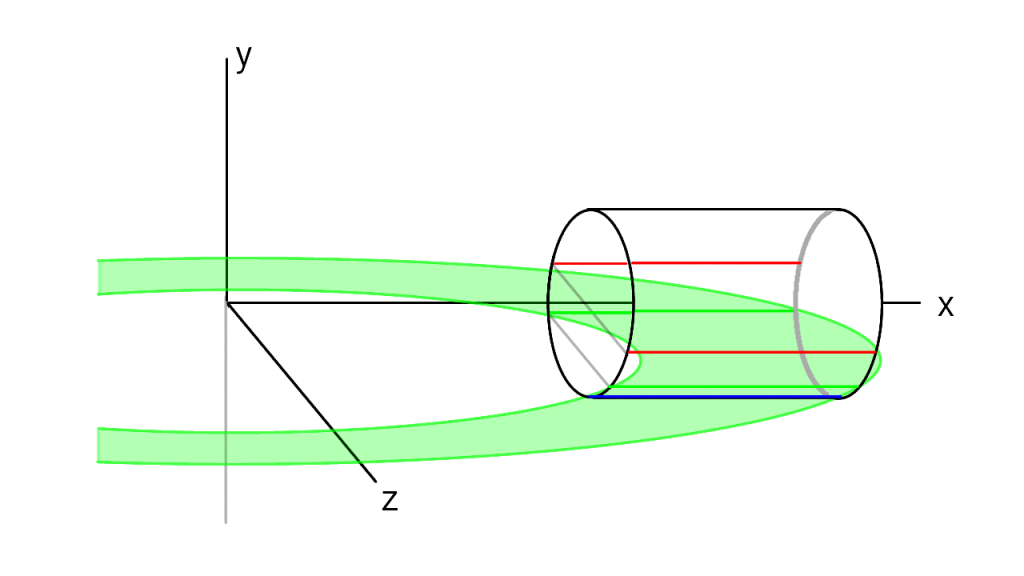
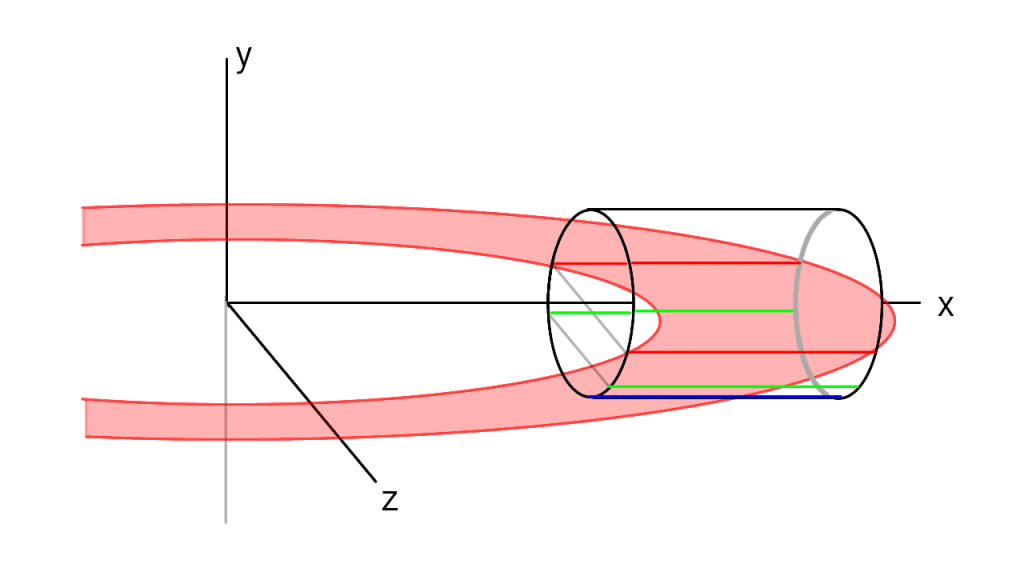
青→緑→赤となるにつれて、円筒内への侵入具合が大きくなっていきます。
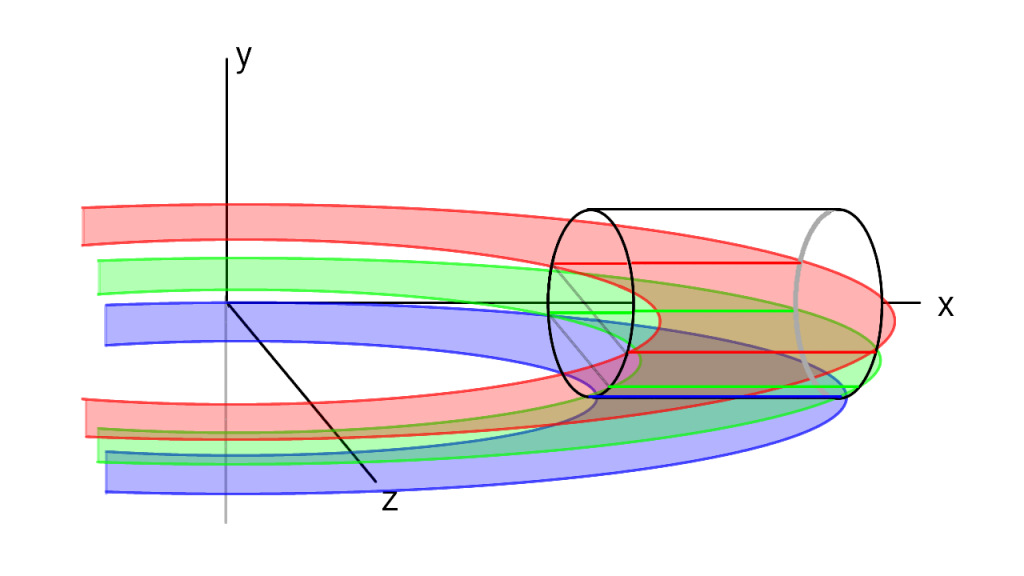
3つ重ねてみるとこんな感じ。
ちょっと分かりにくいですが、$y$によって軌跡の内半径と外半径が異なるということが伝わればいいなと思います。
- 円筒の回転体、ちくわ型の回転体、円柱の回転体の体積は異なる。
- 外径が同じ場合、円筒の回転体<ちくわ型の回転体<円柱の回転体。
- その理由は、回転軸寄りの淵の軌跡が回転対象内部にえぐりこむことにより、回転体の側面が凹むため。
まとめ
ここでは数式を用いた解説は行いませんが、ポイントとして円柱回転体と円筒回転体は異なるということです。
よく考えないとその違いは見えてきません。
普段から空間図形の3次元的なイメージに慣れておくことが重要ですね!
それでは。
-
前の記事

【図解】グラフの平行移動がなぜマイナスで書かれるか本気で解説してみた 2019.11.25
-
次の記事

【図解】円錐の回転体を図示してみよう【東大2017,阪大2013】 2020.01.07















コメントを書く